Principal Component Analysis

Principal Component Analysis#

Principal Component Analysis (PCA) finds the directions in your data where the points are most spread out (maximum variance), allowing you to summarize high-dimensional data using just a few key axes of variation.

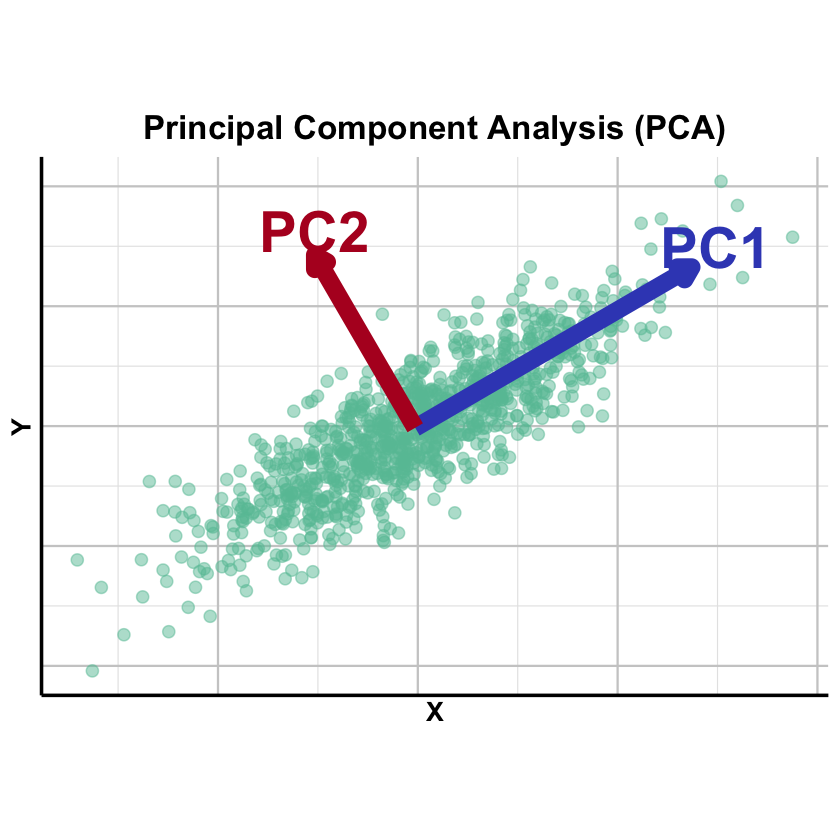
Graphical Summary#

Fig

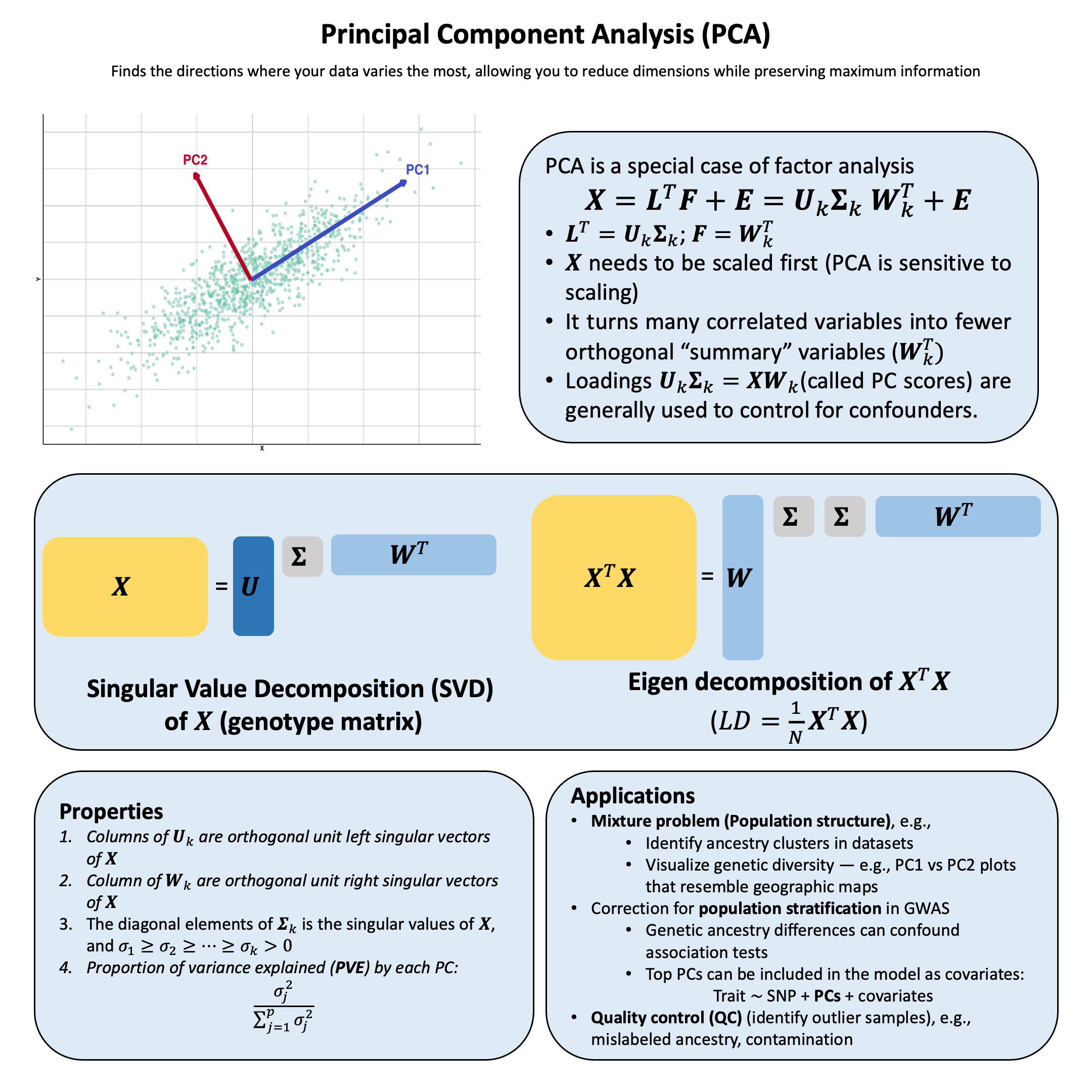
Key Formula#

Let \(\mathbf{X}\) be an \(N \times p\) data matrix (\(N\) observations, \(p\) variables). The singular value decomposition (SVD) of \(\mathbf{X}\) can be written as

\[ \mathbf{X} = \mathbf{L}^T \mathbf{F} + \mathbf{E} = \mathbf{U}_k\mathbf{\Sigma_k}\mathbf{W}_k^T + \mathbf{E} \]

where:

  • \(\mathbf{L}^T=\mathbf{U}_k\mathbf{\Sigma_k}\), \(\mathbf{L}\) can be considered as the loading matrix, as in the context of factor analysis

    • \(\mathbf{U}_k\): \(N \times k\), each column is the left singular vector of \(\mathbf{X}\) (first \(k\) singular vectors)

    • \(\mathbf{\Sigma}_k\): \(k \times k\), a diagonal matrix where each element is the singular value of \(\mathbf{X}\), ordered from largest to smallest (the first \(k\) singular values)

  • \(\mathbf{F}=\mathbf{W}_k^T\) as the factor matrix, as in the context of factor analysis

    • \(\mathbf{W}_k^T\): \(k \times p\), \(\mathbf{W}_k\) consists of the first \(k\) columns of \(\mathbf{W}\), each column of which is the right singular vector of \(\mathbf{X}\)

  • \(\mathbf{E}\): \(N \times p\) reconstruction error (truncation error)

    • If all singular values are used (i.e., \(k=p\)), then \(\mathbf{E}=0\)

Technical Details#

PCA and Factor Analysis#

PCA can be considered as a special case of factor analysis with the following constraints:

  1. \(\mathbf{U}_k\) and \(\mathbf{W}_k\) are both orthogonal matrix

  2. Each column of \(\mathbf{U}_k\) is a unit vector of length \(N\), the left singular vector of \(\mathbf{X}\)

  3. The diagonal elements (\(\sigma_1, \dots, \sigma_k\)) of the top part of \(\mathbf{\Sigma}_k\) is the singular values of \(\mathbf{X}\), and \(\sigma_1 \geq \sigma_2 \geq \dots \geq \sigma_k > 0\)

  4. Each column of \(\mathbf{W}_k\) is a unit vector of length \(p\), the right singular vector of \(\mathbf{X}\)

When conducting PCA, we order the singular values by the variance \(\sigma_1 \geq \sigma_2 \geq \dots \geq \sigma_k > 0\) to reach the variance maximization by selecting the first \(k\) singular vectors.

PCA and Regression#

Factor analysis in general is similar to the concept of regression, which we introduce in Lecture: ordinary least squares. The fundamental difference is that in regression \(\mathbf{X}\) and \(\mathbf{Y}\) is fixed and the goal is to estimate \(\beta\), but in factor analysis, only \(\mathbf{Y}\) is fixed and both \(\mathbf{L}\) and \(\mathbf{F}\) is to be estimated to reach the best performance.

Specifically, PCA starts to solve for the first column of \(\mathbf{L}\) and row of \(\mathbf{F}\) that minimize the squared error in predicting \(\mathbf{X}\); the second principal component then fits the “residual” error that is left behind after removing the first principal component: i.e., it minimizes the squared error in \(\mathbf{X}\); so on, for subsequent PCs. Please refer to HGBook (box on page 191) for more details.

Scaling#

PCA is sensitive to the scaling of the variables. Mathematically this sensitivity comes from the way a rescaling changes the sample‑covariance matrix that PCA diagonalises. So in practice one needs to scale (both centered and unit variance) the matrix before performing PCA.

Eigen Decomposition and Variance Explained#

When \(\mathbf{X}\) is scaled (zero mean, unit variance), \(\mathbf{X}^T\mathbf{X}/(N-1)\) equals the sample covariance matrix. PCA via eigendecomposition finds the eigenvectors of this covariance matrix:

\[ \mathbf{X}^T\mathbf{X} = (\mathbf{W}\mathbf{\Sigma}\mathbf{U}^T)(\mathbf{U}\mathbf{\Sigma}\mathbf{W}^T) = \mathbf{W}\mathbf{\Sigma}^T\mathbf{\Sigma}\mathbf{W}^T = \mathbf{W}\mathbf{\Lambda}\mathbf{W}^T \]

where \(\mathbf{\Lambda} = \mathbf{\Sigma}^T\mathbf{\Sigma}\) is a \(p\times p\) diagonal matrix of eigenvalues. The eigenvalues relate to singular values by \(\lambda_k = \sigma_k^2\) and represent variance explained along each principal direction. The proportion of variance explained by the first \(k\) PCs is:

\[ \text{PVE}=\frac{\sum_{j=1}^k \lambda_j}{\sum_{j=1}^p \lambda_j} = \frac{\sum_{j=1}^k \sigma_j^2}{\sum_{j=1}^p \sigma_j^2} \]

In practice, SVD of \(\mathbf{X}\) is preferred for numerical stability, but eigendecomposition of \(\mathbf{X}^T\mathbf{X}\) provides useful perspective on the variance structure.

Terminology#

In PCA, we focus on the top \(k\) PC loadings \(\mathbf{U}_k\mathbf{\Sigma_k}\) for each individual, denoted \(\text{PC}_1, \text{PC}_2, ..., \text{PC}_k\). These are commonly visualized by plotting \(\text{PC}_1\) vs \(\text{PC}_2\) to detect outliers or population stratification. This reduces dimensionality from \(p\) to \(k\) while maximizing retained information through orthogonal components.

Example#

You have genotyped individuals and want to determine: Do they share the same genetic ancestry, or do they come from different populations? Population structure is a major confounder in association studies, making this a fundamental question in population genetics and forensics.

PCA can reveal population structure without prior knowledge of population labels. Using the same setting as Lecture: factor analysis, we’ll show how PCA easily detects four distinct groups of individuals through their principal components.

Setup#

This is the same generation as we did in the Example 1 in Lecture: factor analysis.

rm(list=ls())
set.seed(74)

N <- 50  # Number of individuals
p <- 100  # Number of markers (SNPs)
k <- 2   # Number of ancestral populations

# Create L matrix with very distinct population frequencies
F_true <- matrix(0, nrow = k, ncol = p)
# Population 1: generally higher frequencies in the first 50 SNPS, lower frequencies in the last 50
F_true[1, 1:50] <- runif(50, 0.9, 0.95)
F_true[1, 51:100] <- runif(50, 0.05, 0.1)

# Population 2: inverse pattern
F_true[2, 1:50] <- runif(50, 0.05, 0.3)
F_true[2, 51:100] <- runif(50, 0.8, 0.95)

# Add row and column names
colnames(F_true) <- paste0("SNP", 1:p)
rownames(F_true) <- paste0("POP", 1:k)

transpose_L_true <- matrix(0, nrow = N, ncol = k)

# Individuals 1-15: Pure Pop1
transpose_L_true[1:15, 1] <- 1.0
transpose_L_true[1:15, 2] <- 0.0

# Individuals 16-30: Pure Pop2
transpose_L_true[16:30, 1] <- 0.0
transpose_L_true[16:30, 2] <- 1.0

# Individuals 31-40: Pop1-Pop2 admixture (80-20)
transpose_L_true[31:40, 1] <- 0.8
transpose_L_true[31:40, 2] <- 0.2
# Individuals 41-50: Pop1-Pop2 admixture (30-70)
transpose_L_true[41:50, 1] <- 0.3
transpose_L_true[41:50, 2] <- 0.7

# Add row and column names
rownames(transpose_L_true) <- paste0("IND", 1:N)
colnames(transpose_L_true) <- paste0("POP", 1:k)

X_raw <- matrix(0, nrow = N, ncol = p)

for (i in 1:N) {
  for (j in 1:p) {
    # Expected frequency = weighted average of population frequencies
    p_ij <- sum(transpose_L_true[i, ] * F_true[ , j])
    
    # Sample genotype (0, 1, or 2 copies)
    X_raw[i,j] <- rbinom(1, size = 2, prob = p_ij)
  }
}

# Add row and column names
rownames(X_raw) <- paste0("IND", 1:N)
colnames(X_raw) <- paste0("SNP", 1:p)

As described above, we need to scale the X_raw first before performing PCA:

X <- scale(X_raw, center = TRUE, scale = TRUE)

PCA#

Now we apply PCA to the genotype matrix \(\mathbf{X}\) to discover the population structure.

pca_result <- prcomp(X, center = FALSE, scale. = FALSE)

PVE by the top PCs#

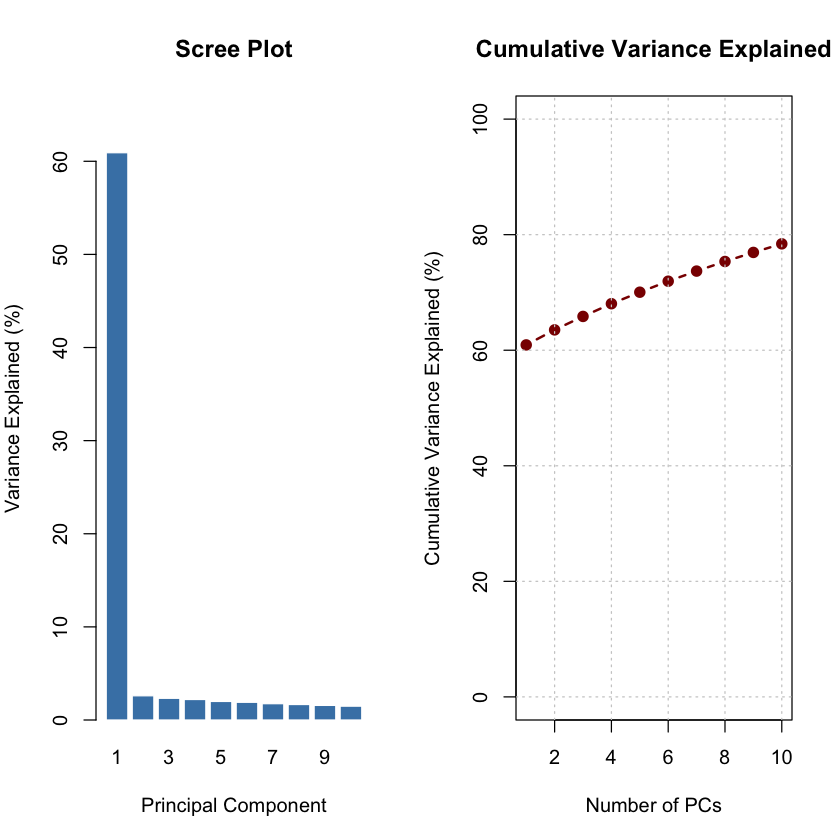
The scree plot shows that the first principal component captures the majority of variance, indicating strong population differentiation.

# Extract principal component scores
pc_scores <- pca_result$x

# Calculate variance explained by each PC
variance_explained <- (pca_result$sdev^2) / sum(pca_result$sdev^2) * 100

cat("Variance explained by top 5 PCs:\n")
for (i in 1:5) {
  cat(sprintf("PC%d: %.2f%%\n", i, variance_explained[i]))
}
cat("\n")

Variance explained by top 5 PCs:
PC1: 60.92%
PC2: 2.60%
PC3: 2.33%
PC4: 2.20%
PC5: 1.99%

# Create scree plot
par(mfrow = c(1, 2), mar = c(5, 4, 4, 2))

# Barplot of variance explained
barplot(variance_explained[1:10],
        names.arg = 1:10,
        xlab = "Principal Component",
        ylab = "Variance Explained (%)",
        main = "Scree Plot",
        col = "steelblue",
        border = "white",
        ylim = c(0, max(variance_explained[1:10]) * 1.1))

# Cumulative variance explained
cumvar <- cumsum(variance_explained[1:10])
plot(1:10, cumvar,
     type = "b",
     pch = 19,
     col = "darkred",
     lwd = 2,
     xlab = "Number of PCs",
     ylab = "Cumulative Variance Explained (%)",
     main = "Cumulative Variance Explained",
     ylim = c(0, 100))
grid(col = "gray80")
_images/f6a1006e35388f06d1e570f33e00a82465933f97fe493d6b666b8496d0cdedcd.png

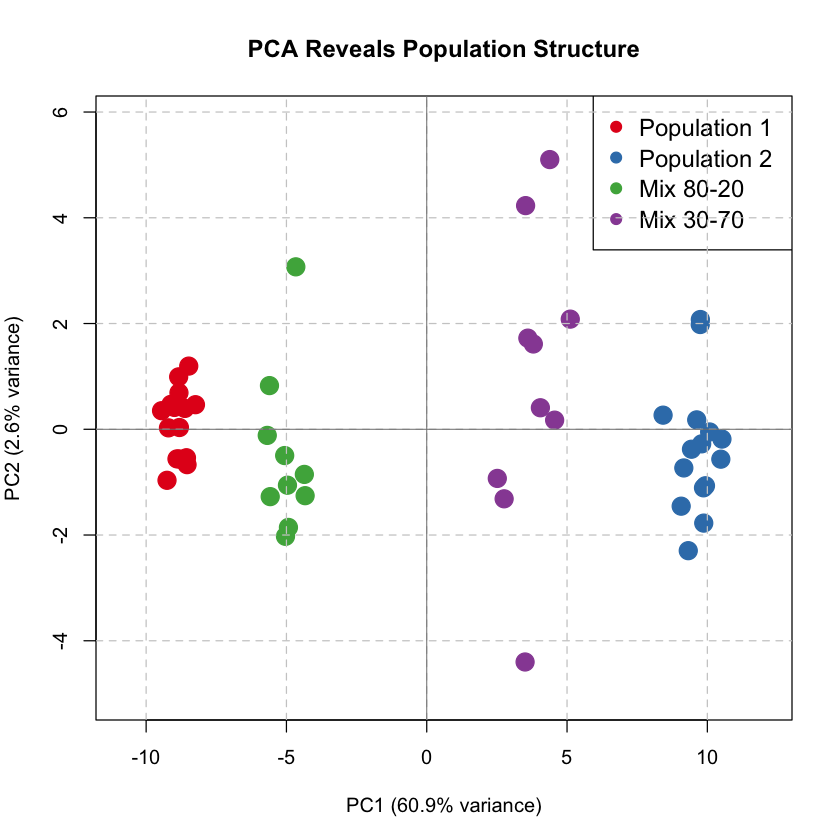
PC1 vs PC2 Colored by Population#

We plot the first two principal components, coloring individuals by their true population origin (which PCA discovers automatically!).

# Define colors for populations
pop_labels <- c(rep("Population 1", 15), rep("Population 2", 15), rep("Mix 80-20", 10), rep("Mix 30-70", 10))
pop_colors <- c("Population 1" = "#E41A1C", "Population 2" = "#377EB8", "Mix 80-20" = "#4DAF4A", "Mix 30-70" = "#984EA3")

# Create scatter plot: PC1 vs PC2
par(mfrow = c(1, 1), mar = c(5, 4, 4, 2))

plot(pc_scores[, 1], pc_scores[, 2],
     col = pop_colors[pop_labels],
     pch = 19, cex = 2,
     xlab = sprintf("PC1 (%.1f%% variance)", variance_explained[1]),
     ylab = sprintf("PC2 (%.1f%% variance)", variance_explained[2]),
     main = "PCA Reveals Population Structure",
     xlim = range(pc_scores[, 1]) * 1.15,
     ylim = range(pc_scores[, 2]) * 1.15)

legend("topright", 
       legend = names(pop_colors),
       col = pop_colors, 
       pch = 19, 
       cex = 1.2,
       bty = "o")

grid(col = "gray80", lty = 2)
abline(h = 0, col = "gray50", lty = 1, lwd = 0.8)
abline(v = 0, col = "gray50", lty = 1, lwd = 0.8)
_images/810ced0cf1ccd8b72795a45a2ab029e47a73ef596dc0a51e06e7f8e1e67e69e1.png

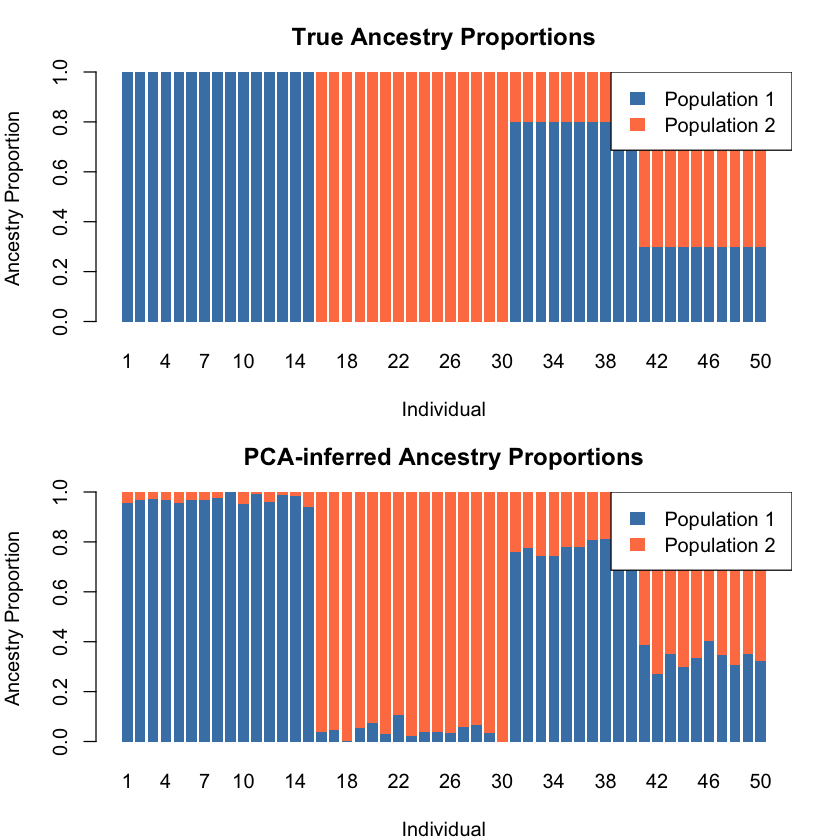
From Mixture to Admixture#

PCA captures four clusters here, but the data represents an admixture problem — individuals have varying proportions of two ancestries. As a factor analysis method, PCA can infer ancestry proportions from PC scores when population structure dominates variation (PC1 explains most variance) and populations are well-separated.

The \(k\)-th PC score for individual \(i\) is a linear combination of genotypes weighted by \(\mathbf{W}_k\):

\[ \text{PC score}_{i,k} = \sum_{j=1}^p \mathbf{X}_{i,j} \cdot \mathbf{W}_{j,k} \]

These scores can be scaled to [0,1] to represent ancestry proportions.

Both ADMIXTURE and PCA model allele frequencies as linear combinations of \(k\) factors:

  • ADMIXTURE: Expected allele frequency = ancestry proportions \(\times\) population allele frequencies

  • PCA: Weighted combination of \(p\) variants implicitly represents ancestry through \(\mathbf{W}_k\)

For detailed PCA-STRUCTURE relationships, see Pritchard’s HGBook (pages 190-192). STRUCTURE and ADMIXTURE differ in statistical frameworks (discussed in Lecture: Bayesian versus Frequentist).

# Find the range of PC1 scores
pc1_min <- min(pc_scores[, 1])
pc1_max <- max(pc_scores[, 1])

# Estimate ancestry proportions by rescaling PC1 to [0, 1]
# This assumes: Pop1 is at pc1_min, Pop2 is at pc1_max
# Ancestry proportion for Pop2 = (PC1_score - pc1_min) / (pc1_max - pc1_min)
ancestry_pop1_pca <- (pc_scores[, 1] - pc1_min) / (pc1_max - pc1_min)
ancestry_pop2_pca <- 1 - ancestry_pop1_pca

# Create a matrix similar to the ADMIXTURE transpose_L matrix
transpose_L_pca <- t(rbind(ancestry_pop1_pca, ancestry_pop2_pca))
colnames(transpose_L_pca) <- c("POP1", "POP2")
rownames(transpose_L_pca) <- rownames(X)

# Calculate correlation between true and PCA-inferred ancestry
cor_pop1 <- cor(transpose_L_true[ , 1], transpose_L_pca[ , "POP1"])
cor_pop2 <- cor(transpose_L_true[ , 2], transpose_L_pca[ , "POP2"])

cat("Correlation between true and PCA-inferred ancestry proportions:\n")
cat(sprintf("Population 1: %.4f\n", cor_pop1))
cat(sprintf("Population 2: %.4f\n", cor_pop2))

Correlation between true and PCA-inferred ancestry proportions:
Population 1: -0.9976
Population 2: -0.9976

Since the correlations are all close to -1, we need to flip the populations.

transpose_L_pca_flipped <- transpose_L_pca[, c("POP2", "POP1")]

# Visualize the comparison using same style as ADMIXTURE
par(mfrow = c(2, 1), mar = c(4, 4, 3, 2))

# True ancestry
barplot(t(transpose_L_true), col = c("steelblue", "coral"), border = NA,
        main = "True Ancestry Proportions",
        xlab = "Individual", ylab = "Ancestry Proportion",
        names.arg = 1:N)
legend("topright", legend = c("Population 1", "Population 2"),
       fill = c("steelblue", "coral"), border = NA)

# PCA-inferred ancestry
barplot(t(transpose_L_pca_flipped), col = c("steelblue", "coral"), border = NA,
        main = "PCA-inferred Ancestry Proportions",
        xlab = "Individual", ylab = "Ancestry Proportion",
        names.arg = 1:N)
legend("topright", legend = c("Population 1", "Population 2"),
       fill = c("steelblue", "coral"), border = NA)
_images/faeec2687a4d8738913d964b6a642cc346f3964a3350a3986faa65344b8d936d.png

While PCA can visualize population structure, for admixture analysis it is better to use the ADMIXTURE model introduced in Factor Analysis. Here’s why:

  • PCA is a descriptive method: PCA finds the directions of maximum variance in the data but does not provide a statistical model of how the data was generated

  • ADMIXTURE is a generative model: ADMIXTURE explicitly models the genetic mixture as a weighted combination of ancestry components: \(\mathbf{X} = \mathbf{L}^T\mathbf{F} + \mathbf{E}\) (check Factor Analysis for more details)

Interpretation of Loadings for PC1#

Here we show that actually the loading for PC1 actually captures the difference of the allele frequencies between the two ancestries:

# Extract PC loadings (weights for each SNP)
pc1_loadings <- pca_result$rotation[, 1]
pc2_loadings <- pca_result$rotation[, 2]

# Calculate allele frequency for each population at each SNP
pop1_freq <- colMeans(X_raw[1:15, ]) / 2   # Pure Population 1
pop2_freq <- colMeans(X_raw[16:30, ]) / 2  # Pure Population 2

# Calculate allele frequency difference between populations
freq_diff <- pop2_freq - pop1_freq

# Show correlations
cor_pc1_freqdiff <- cor(pc1_loadings, freq_diff)

cat("\n=== PC Loadings and Allele Frequency Differences in the Raw Data ===\n")
cat(sprintf("Correlation between PC1 loadings and freq differences (raw data): %.4f\n", cor_pc1_freqdiff))

=== PC Loadings and Allele Frequency Differences in the Raw Data ===
Correlation between PC1 loadings and freq differences (raw data): 0.9975

And this correlation persists after the scaling of input data as well:

# Calculate allele frequency for each population at each SNP
pop1_freq_scaled <- colMeans(X[1:15, ]) / 2   # Pure Population 1
pop2_freq_scaled <- colMeans(X[16:30, ]) / 2  # Pure Population 2

# Calculate allele frequency difference between populations
freq_diff_scaled <- pop2_freq_scaled - pop1_freq_scaled

# Show correlations
cor_pc1_freqdiff_scaled <- cor(pc1_loadings, freq_diff_scaled)

cat("\n=== PC Loadings and Allele Frequency Differences After Scaling the Data ===\n")
cat(sprintf("Correlation between PC1 loadings and freq differences (scaled data): %.4f\n", cor_pc1_freqdiff_scaled))
cat("\n")

=== PC Loadings and Allele Frequency Differences After Scaling the Data ===
Correlation between PC1 loadings and freq differences (scaled data): 0.9985

Supplementary#

Graphical Summary#

library(ggplot2)

# Set seed for reproducibility
set.seed(42)

# Generate correlated 2D data with PC1 >> PC2
n <- 1000
theta <- pi/6  # 30 degree tilt

# Create elongated cloud - PC1 much longer than PC2
x <- rnorm(n, 0, 3)    # Large variance for PC1 direction
y <- rnorm(n, 0, 0.8)  # Small variance for PC2 direction

# Rotate to create diagonal spread
X_original <- x * cos(theta) - y * sin(theta)
Y_original <- x * sin(theta) + y * cos(theta)

data <- data.frame(X = X_original, Y = Y_original)

# Perform PCA
pca <- prcomp(data, center = TRUE, scale. = FALSE)

# Get PC directions - flip if needed
pc1_direction <- -pca$rotation[, 1]  
pc2_direction <- -pca$rotation[, 2]  

# Scale for visualization
scale_factor1 <- 8
scale_factor2 <- 5
pc1_end <- scale_factor1 * pc1_direction
pc2_end <- scale_factor2 * pc2_direction

# Get the center (mean)
center_x <- mean(X_original)
center_y <- mean(Y_original)

# Create the plot
p_PCA <- ggplot(data, aes(x = X, y = Y)) +
  geom_point(color = "#66C2A5", alpha = 0.5, size = 3) +
  
  # PC1 arrow (blue) - use annotate instead of geom_segment
  annotate("segment", 
           x = center_x, y = center_y, 
           xend = center_x + pc1_end[1], 
           yend = center_y + pc1_end[2],
           arrow = arrow(length = unit(0.3, "cm"), type = "closed"),
           color = "#3B4CC0", linewidth = 5) +
  annotate("text", x = center_x + pc1_end[1] + 0.6, 
           y = center_y + pc1_end[2] + 0.5, 
           label = "PC1", color = "#3B4CC0", size = 12, fontface = "bold") +
  
  # PC2 arrow (purple) - use annotate instead of geom_segment
  annotate("segment", 
           x = center_x, y = center_y, 
           xend = center_x + pc2_end[1], 
           yend = center_y + pc2_end[2],
           arrow = arrow(length = unit(0.3, "cm"), type = "closed"),
           color = "#B40426", linewidth = 5) +
  annotate("text", x = center_x + pc2_end[1], 
           y = center_y + pc2_end[2] + 0.6, 
           label = "PC2", color = "#B40426", size = 12, fontface = "bold") +
  
  # Styling
  labs(title = "Principal Component Analysis (PCA)",
       x = "X", y = "Y") +
  theme_minimal(base_size = 14) +
  theme(
    plot.title = element_text(hjust = 0.5, size = 20, face = "bold"),
    axis.title.x = element_text(size = 16, face = "bold"),
    axis.title.y = element_text(size = 16, face = "bold"),
    axis.text = element_blank(),
    panel.grid.major = element_line(color = "gray80"),
    panel.grid.minor = element_line(color = "gray90"),
    axis.line = element_line(color = "black", linewidth = 1),
    plot.background = element_rect(fill = "transparent", color = NA),
    panel.background = element_rect(fill = "transparent", color = NA)
  ) +
  coord_fixed(ratio = 1)
  
# Save with transparent background
ggsave("./figures/PCA.png", plot = p_PCA, width = 18, height = 12, 
       units = "in", dpi = 300, bg = "transparent")

print(p_PCA)
_images/2bf60687f6397a3a07485df3fc3eba576bbf5080cd47533b45cecf81bab95186.png

Extended Reading#

Contents