Linear Mixed Model#
When we want to study a specific genetic variant as a fixed effect but know there are countless unmeasured factors affecting our trait, linear mixed models offer a practical solution: use a random effect based on genetic similarity to absorb all that unmeasured heterogeneity.
Graphical Summary#
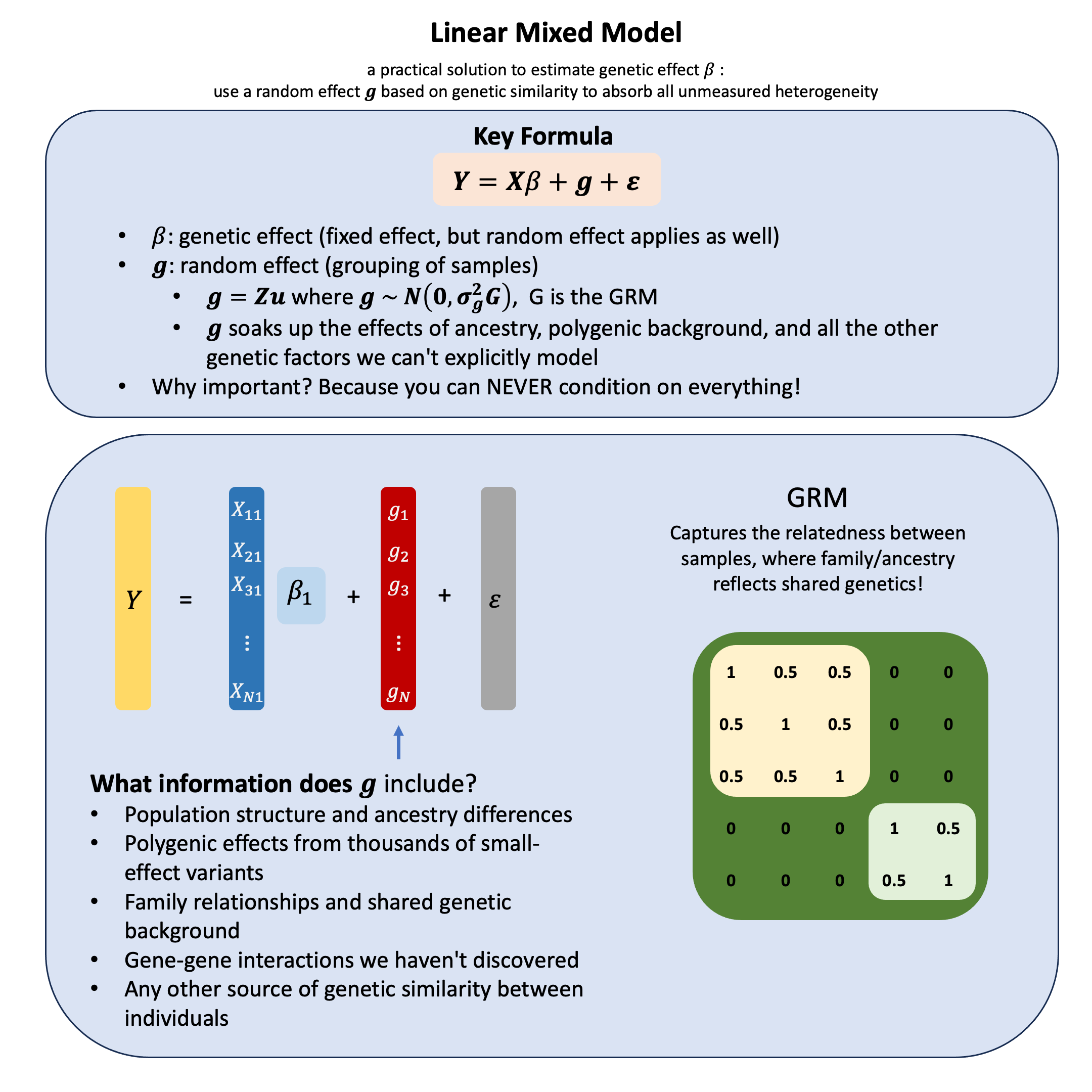
Key Formula#
In the linear mixed model (mixed because it incorporate both the fixed and the random effects), which accurately represent non-independent data structures for a variant,
where:
\(\mathbf{Y}\) is the \(N \times 1\) vector of phenotypes
\(\mathbf{X}\) is the \(N \times 1\) design matrix for fixed effects (e.g., the specific genetic variant we’re testing, plus measurable covariates like age and sex)
\(\beta\) is the scalar of genetic effect coefficient (unknown, to be estimated, generally fixed but also can be random)
\(\mathbf{g} \sim N(0,\sigma^2_g\mathbf{G})\) is the \(N \times 1\) vector of random effects that captures all the genetic factors we can’t or don’t want to model explicitly - population structure, polygenic background, family relationships, and countless unknown genetic influences
\(\boldsymbol{\epsilon}\) is the \(N \times 1\) vector of residual errors, where \(\boldsymbol{\epsilon} \sim N(0, \sigma^2_e\mathbf{I})\)
Technical Details#
Random Effects Decomposition: \(\mathbf{g}\) and \(\mathbf{Zu}\)#
For any genetic variant, we cannot model all contributing factors explicitly (age, sex, ancestry, thousands of genes, unknown factors, etc). Instead of the complete model:
We approximate it as:
where \(\mathbf{g}\) soaks up the effects of ancestry, polygenic background, and all the other genetic factors we can’t explicitly model.
The random effects term g can be decomposed as:
where:
\(\mathbf{G}\) is the genetic relationship matrix (GRM) that measures genetic similarity between individuals, effectively capturing all the unmeasured genetic factors through genome-wide similarity patterns
\(\mathbf{Z}\) is the \(N \times M\) genotype matrix for \(M\) genetic variants
\(\mathbf{u} \sim N(0, \sigma_u^2\mathbf{I})\) is a \(M \times 1\) vector of random SNP effects
This formulation is formally known as the infinitesmal model
Popular LMM Methods in Statistical Genetics#
Method |
Purpose |
Key Innovation |
Scale/Application |
|---|---|---|---|
GCTA |
Heritability estimation and association testing |
Uses genome-wide SNPs to construct genetic relationship matrix (GRM) |
\(h^2 = \frac{\sigma^2_u}{\sigma^2_u + \sigma^2_e}\) estimation |
GEMMA |
Fast genome-wide association studies with population structure control |
Efficient eigendecomposition for kinship correction |
Computationally efficient for large-scale data |
BOLT-LMM |
Ultra-fast mixed model association testing |
Bayesian sparse linear mixed model with Monte Carlo sampling |
Hundreds of thousands of individuals |
SAIGE |
Association testing for binary and quantitative traits |
Saddlepoint appeoximation for unbalanced case-control data |
Large-scale biobanks with rare outcomes |
REGENIE |
Whole genome regression with prediction |
Two-step ridge regression avoiding explicit mixed model |
Ultra-large biobanks (millions of samples) |
Example#
What happens when we acknowledge that our trait is influenced not just by one specific variant, but also by a “genetic background” from all the other variants we’re not explicitly testing? Let’s see how linear mixed models capture this reality.
We’ll use the same 5 individuals, but now we’ll model two sources of genetic influence: a fixed effect from one specific variant we’re studying, plus a random polygenic effect that represents the combined influence of all variants acting as genetic background. How much does each component contribute to the total genetic influence on our trait?
Setup#
# Clear the environment
rm(list = ls())
set.seed(13)
library(MASS) # For mvrnorm function
# Define genotypes for 5 individuals at 3 variants
# These represent actual alleles at each position
# For example, Individual 1 has genotypes: CC, CT, AT
genotypes <- c(
"CC", "CT", "AT", # Individual 1
"TT", "TT", "AA", # Individual 2
"CT", "CT", "AA", # Individual 3
"CC", "TT", "AA", # Individual 4
"CC", "CC", "TT" # Individual 5
)
# Reshape into a matrix
N = 5
M = 3
geno_matrix <- matrix(genotypes, nrow = N, ncol = M, byrow = TRUE)
rownames(geno_matrix) <- paste("Individual", 1:N)
colnames(geno_matrix) <- paste("Variant", 1:M)
alt_alleles <- c("T", "C", "T")
# Convert to raw genotype matrix using the additive model
Xraw_additive <- matrix(0, nrow = N, ncol = M) # count number of non-reference alleles
rownames(Xraw_additive) <- rownames(geno_matrix)
colnames(Xraw_additive) <- colnames(geno_matrix)
for (i in 1:N) {
for (j in 1:M) {
alleles <- strsplit(geno_matrix[i,j], "")[[1]]
Xraw_additive[i,j] <- sum(alleles == alt_alleles[j])
}
}
X <- scale(Xraw_additive, center = TRUE, scale = TRUE)
Linear Mixed Model#
We generate the data according to a linear mixed model:
# Linear Mixed Model: Y = X*beta + g + epsilon
# where g = Z*u represents random polygenic effects
# Fixed effect for variant 1
beta <- 0.8 # Fixed effect size for variant 1
# Create Genetic Relationship Matrix (GRM) using all variants
# GRM = (1/M) * X_raw * X_raw^T, where X_raw is the standardized genotype matrix
GRM <- (1/M) * X %*% t(X)
cat("Genetic Relationship Matrix (GRM):\n")
GRM
# Generate random polygenic effects: g ~ N(0, sigma_u^2 * GRM)
sigma_u <- 0.5 # Standard deviation of random effects
g <- mvrnorm(n = 1, mu = rep(0, N), Sigma = sigma_u^2 * GRM)
g <- as.vector(g)
# Residual errors
sigma_e <- 0.3 # Standard deviation of residual errors
epsilon <- rnorm(N, mean = 0, sd = sigma_e)
# Generate phenotype with both fixed and random effects
Y <- X[, 1] * beta + g + epsilon
Genetic Relationship Matrix (GRM):
| Individual 1 | Individual 2 | Individual 3 | Individual 4 | Individual 5 | |
|---|---|---|---|---|---|
| Individual 1 | 0.23571429 | -0.5261905 | -0.18095238 | -0.02619048 | 0.4976190 |
| Individual 2 | -0.52619048 | 1.2714286 | 0.30714286 | 0.10476190 | -1.1571429 |
| Individual 3 | -0.18095238 | 0.3071429 | 0.23571429 | -0.02619048 | -0.3357143 |
| Individual 4 | -0.02619048 | 0.1047619 | -0.02619048 | 0.60476190 | -0.6571429 |
| Individual 5 | 0.49761905 | -1.1571429 | -0.33571429 | -0.65714286 | 1.6523810 |
Estimating PVE#
We can estimate the PVE again by each component:
# In LMM, total genetic variance = fixed effects variance + random effects variance
# Fixed genetic component from variant 1
G_fixed <- X[, 1] * beta
# Random genetic component (polygenic background)
G_random <- g
# Total genetic component
G_total <- G_fixed + G_random
# Calculate variance components
var_G_fixed <- var(G_fixed)
var_G_random <- var(G_random)
var_G_total <- var(G_total)
var_Y <- var(Y)
# PVE calculations
PVE_fixed <- var_G_fixed / var_Y # PVE from fixed effects only
PVE_random <- var_G_random / var_Y # PVE from random effects only
PVE_total <- var_G_total / var_Y # Total PVE
cat("PVE Components:\n")
cat("PVE_fixed (variant 1) =", round(PVE_fixed, 4), "\n")
cat("PVE_random (polygenic) =", round(PVE_random, 4), "\n")
cat("PVE_total =", round(PVE_total, 4), "\n\n")
PVE Components:
PVE_fixed (variant 1) = 1.3277
PVE_random (polygenic) = 1.2751
PVE_total = 0.6073
Note that the same framework applies when the genetic effect \(\beta\) is modeled as a random effect rather than fixed.