Meta-Analysis Fixed Effect

Meta-Analysis Fixed Effect#

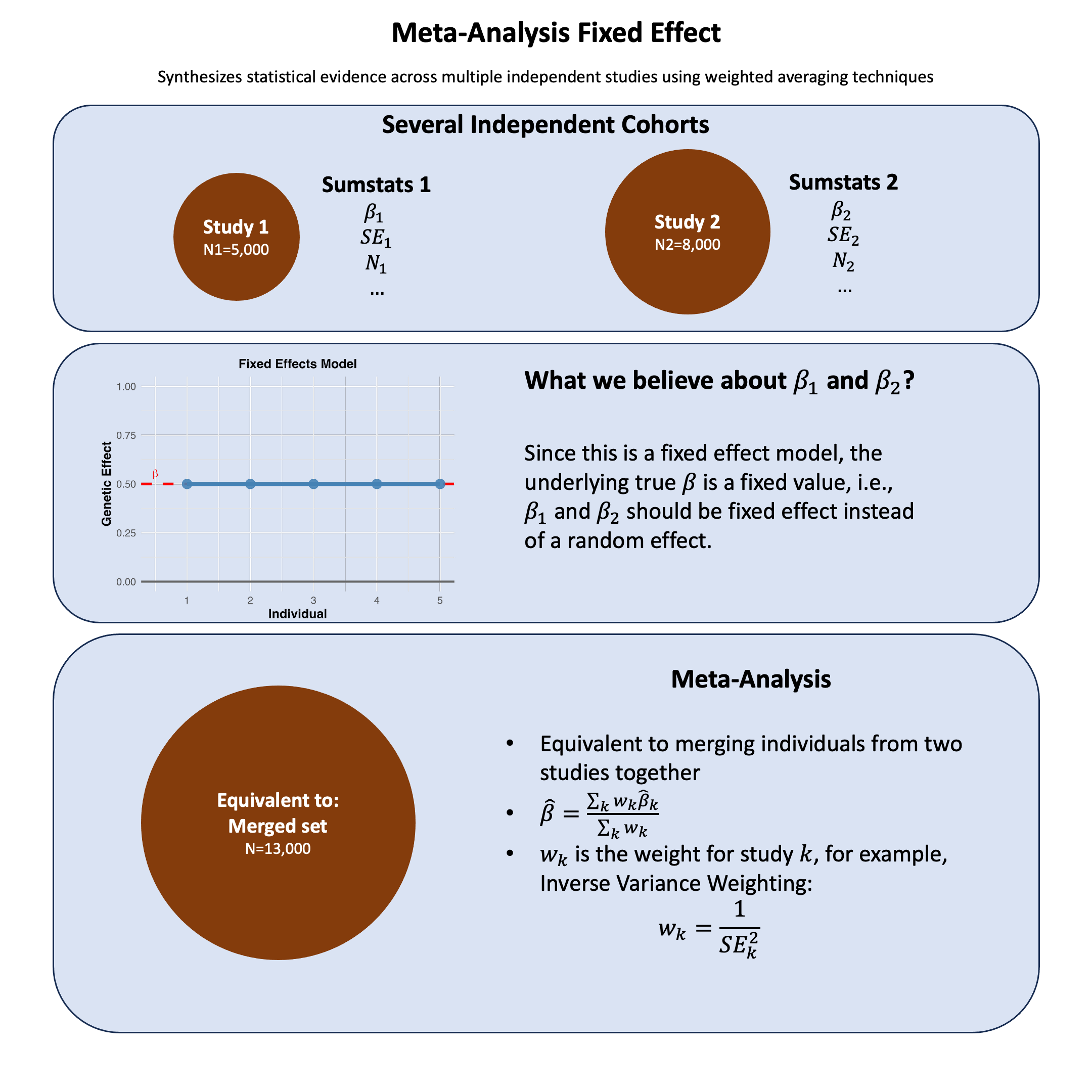
Fixed-effect meta-analysis combines study-specific estimates under the assumption of a common fixed true effect, making it mathematically equivalent to analyzing all individuals as if they came from a single pooled dataset.

Graphical Summary#

Fig

Key Formula#

In meta-analysis, the weighted mean effect size for a fixed-effects model is calculated as:

\[\hat{\beta} = \frac{\sum_{k=1}^{K} w_k \hat{\beta}_k}{\sum_{k=1}^{K} w_k}\]

Where:

  • \(\hat{\beta}\) is the combined effect estimate across all studies

  • \(\hat{\beta}_i\) is the effect estimate from study \(k\)

  • \(w_k\) is the weight assigned to study \(k\)

  • \(K\) is the number of studies

Technical Details#

Why Meta-Analysis?#

Meta-analysis addresses individual study limitations (small samples, random variation, limited generalizability) by combining results to achieve larger effective sample sizes, more precise estimates, and broader population representation.

Inverse-Variance Weighting#

The key insight is that not all studies should contribute equally. Studies contribute based on their precision:

\[ w_k = \frac{1}{\text{SE}_k^2} \]

Where \(\text{SE}_k\) is the standard error of study \(k\).

Large, precise studies (small SE) receive high weight; small, imprecise studies (large SE) receive low weight.

The Fixed-Effects Assumption#

Assumes all studies estimate the same true effect—differences are only due to sampling variation.

Use when: Studies are similar in design, population, and methods with low heterogeneity.

Avoid when: Studies differ substantially or show high heterogeneity (use random-effects instead).

Limitations#

  • Garbage in, garbage out: Meta-analysis cannot fix poorly designed individual studies

  • Publication bias: Published studies may not represent all conducted research

  • Population differences: Genetic effects may genuinely differ across populations

Example#

This example demonstrates fixed-effects meta-analysis for a single genetic variant across two cohorts (N=5,000 and N=8,000). We combine effect estimates using inverse-variance weighting and compare the meta-analysis result to a pooled analysis of all individuals.

Setup#

rm(list=ls())
set.seed(17)

N1 <- 5000
N2 <- 8000
maf1 <- 0.3
maf2 <- 0.35

variant_pop1 <- rbinom(N1, 2, maf1)
variant_pop2 <- rbinom(N2, 2, maf2)

# 2. Simulate phenotype with fixed effect beta=1 and noise
beta <- 1
y_pop1 <- beta * variant_pop1 + rnorm(N1, 0, 3)
y_pop2 <- beta * variant_pop2 + rnorm(N2, 0, 3)

Regression in Each Population#

lm_pop1 <- lm(y_pop1 ~ variant_pop1)
lm_pop2 <- lm(y_pop2 ~ variant_pop2)

# Extract summary statistics
beta_pop1 <- coef(lm_pop1)["variant_pop1"]
se_pop1 <- summary(lm_pop1)$coefficients["variant_pop1", "Std. Error"]

beta_pop2 <- coef(lm_pop2)["variant_pop2"]
se_pop2 <- summary(lm_pop2)$coefficients["variant_pop2", "Std. Error"]

Meta-analysis#

w1 <- 1 / se_pop1^2
w2 <- 1 / se_pop2^2

beta_meta <- (beta_pop1 * w1 + beta_pop2 * w2) / (w1 + w2)
se_meta <- sqrt(1 / (w1 + w2))
z_meta <- beta_meta / se_meta
p_meta <- 2 * pnorm(-abs(z_meta))

res_meta = data.frame(beta_meta, se_meta, z_meta, p_meta)
rownames(res_meta) = NULL
res_meta
A data.frame: 1 × 4
beta_metase_metaz_metap_meta
<dbl><dbl><dbl><dbl>
1.0044720.0401156825.039382.278672e-138

Merging Populations#

Alternatively we can simply combine all individuals into one and calculate the summary statistics for this variant.

variant_all <- c(variant_pop1, variant_pop2)
y_all <- c(y_pop1, y_pop2)

lm_all <- lm(y_all ~ variant_all)
beta_all <- coef(lm_all)["variant_all"]
se_all <- summary(lm_all)$coefficients["variant_all", "Std. Error"]
z_all <- beta_all / se_all
p_all <- 2 * pnorm(-abs(z_all))

res_merged = data.frame(beta_all, se_all, z_all, p_all)
rownames(res_merged) = NULL
res_merged
A data.frame: 1 × 4
beta_allse_allz_allp_all
<dbl><dbl><dbl><dbl>
1.0025560.0399844725.073649.644327e-139

Comparison of Results#

res_meta
res_merged
A data.frame: 1 × 4
beta_metase_metaz_metap_meta
<dbl><dbl><dbl><dbl>
1.0044720.0401156825.039382.278672e-138
A data.frame: 1 × 4
beta_allse_allz_allp_all
<dbl><dbl><dbl><dbl>
1.0025560.0399844725.073649.644327e-139

The meta-analysis (\(\hat{\beta} = 1.015\), SE = 0.040) and pooled analysis (\(\hat{\beta} = 1.013\), SE = 0.040) yield nearly identical results (after numerical rounding), confirming that fixed-effects meta-analysis is mathematically equivalent to analyzing all individuals together when the true effect is the same across studies.

Contents