Linkage Disequilibrium#
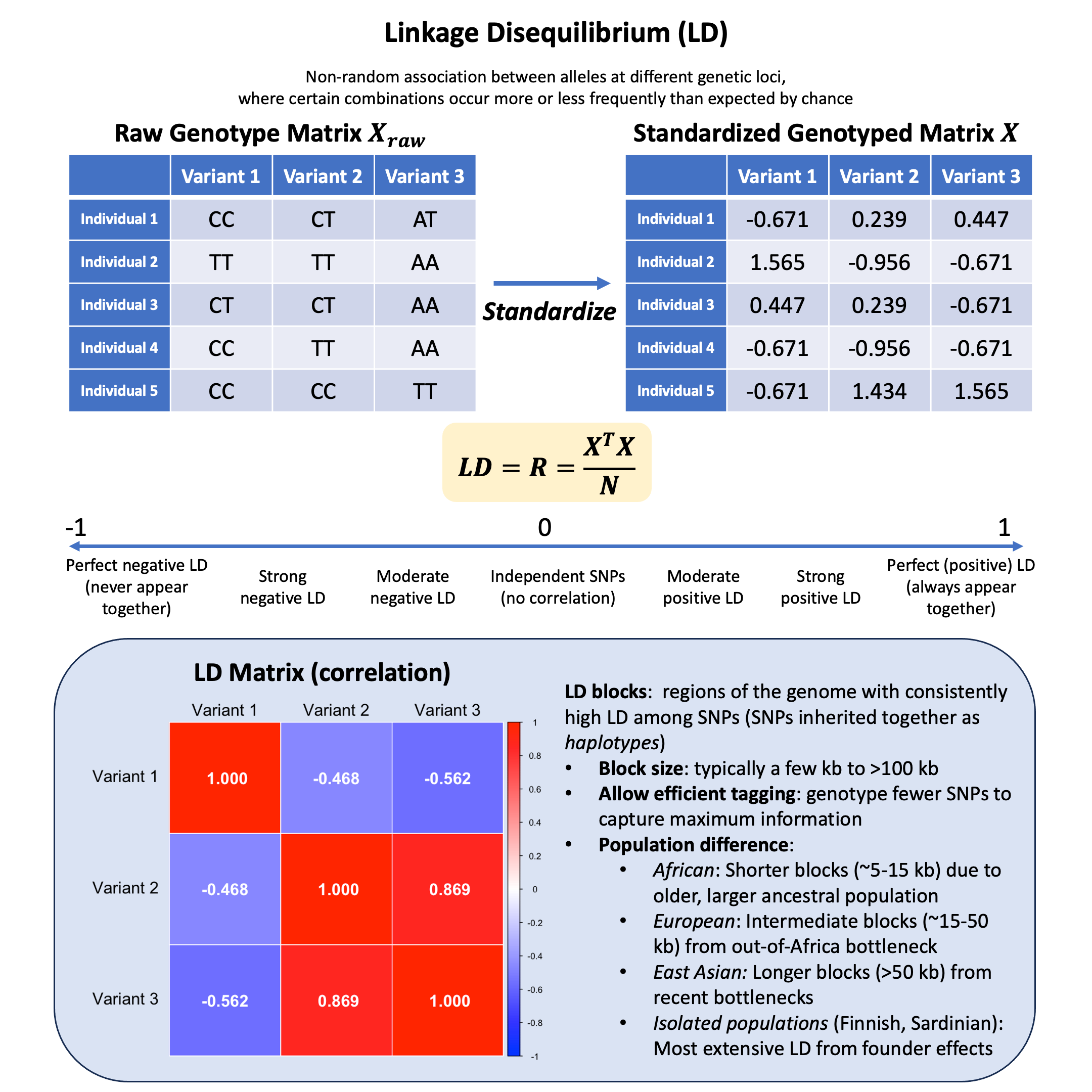
Linkage disequilibrium is the non-random association between alleles at different genetic loci, where certain combinations occur more or less frequently than would be expected by chance if the loci were segregating independently.
Graphical Summary#
Key Formula#
Given a standardized genotype matrix \(\mathbf{X}\) (each column has mean 0 and variance 1), the LD matrix can be computed as:
where:
\(\mathbf{X}\) is the centered genotype matrix
\(N\) is the number of individuals
When \(\mathbf{X}\) is scaled, the covariance matrix is the same as correlation matrix.
Technical Details#
Each element in \(\mathbf{R}\) can be denoted as \(r_{ij}\), the correlation between the \(i\)-th and \(j\)-th variants, ranging from -1 to 1. If it is 1 or -1, it means that the two variants are in perfect LD (markers are perfect proxies for each other). If \(r_{ij}^2=0\), it indicates that no association between markers.
Interpreting LD Values#
High LD (\(r_{ij}^2 > 0.8\)):
Alleles at different loci appear together much more frequently than expected
Frequencies of alleles in high LD are similar to each other
Markers can often serve as proxies for each other in genetic studies
Likely physical proximity on chromosome or recent selection
Less recombination between markers
Moderate LD (\(0.2 < r_{ij}^2 < 0.8\)):
Some association between loci, but not strong enough for perfect tagging
Partial information about one locus given the other
Low LD (\(r_{ij}^2 < 0.2\)):
Loci segregate nearly independently
May indicate distant physical location or sufficient time for recombination
LD Blocks#
LD blocks are genome regions with consistently high LD among SNPs, separated by recombination hotspots. SNPs within a block are highly correlated and inherited together as haplotypes (introduced later in Lecture: factor analysis).
Key features:
Block size: typically a few kb to >100 kb
Define natural haplotype units for analysis
Allow efficient tagging: genotype fewer SNPs to capture maximum information
Visualized as triangular LD heatmaps
Population differences:
African: Shorter blocks (~5-15 kb) due to older, larger ancestral population
European: Intermediate blocks (~15-50 kb) from out-of-Africa bottleneck
East Asian: Longer blocks (>50 kb) from recent bottlenecks
Isolated populations (Finnish, Sardinian): Most extensive LD from founder effects
Example#
We’ve learned how to encode genotypes and standardize them, but what happens when we look at relationships between different variants? Are genetic variants independent of each other, or do they show patterns of correlation?
Let’s use our familiar dataset of 5 individuals at 3 variants to explore how genetic variants can be correlated with each other, and what this correlation matrix tells us about the genetic structure in our sample.
Setup#
# Clear the environment
rm(list = ls())
# Define genotypes for 5 individuals at 3 variants
# These represent actual alleles at each position
# For example, Individual 1 has genotypes: CC, CT, AT
genotypes <- c(
"CC", "CT", "AT", # Individual 1
"TT", "TT", "AA", # Individual 2
"CT", "CT", "AA", # Individual 3
"CC", "TT", "AA", # Individual 4
"CC", "CC", "TT" # Individual 5
)
# Reshape into a matrix
N = 5
M = 3
geno_matrix <- matrix(genotypes, nrow = N, ncol = M, byrow = TRUE)
rownames(geno_matrix) <- paste("Individual", 1:N)
colnames(geno_matrix) <- paste("Variant", 1:M)
alt_alleles <- c("T", "C", "T")
# Convert to raw genotype matrix using the additive / dominant / recessive model
Xraw_additive <- matrix(0, nrow = N, ncol = M) # dount number of non-reference alleles
rownames(Xraw_additive) <- rownames(geno_matrix)
colnames(Xraw_additive) <- colnames(geno_matrix)
for (i in 1:N) {
for (j in 1:M) {
alleles <- strsplit(geno_matrix[i,j], "")[[1]]
Xraw_additive[i,j] <- sum(alleles == alt_alleles[j])
}
}
Then we scale the genotype matrix so that each column (variant) has mean 0 and variance 1.
X <- scale(Xraw_additive, center = TRUE, scale = TRUE)
X
| Variant 1 | Variant 2 | Variant 3 | |
|---|---|---|---|
| Individual 1 | -0.6708204 | 0.2390457 | 0.4472136 |
| Individual 2 | 1.5652476 | -0.9561829 | -0.6708204 |
| Individual 3 | 0.4472136 | 0.2390457 | -0.6708204 |
| Individual 4 | -0.6708204 | -0.9561829 | -0.6708204 |
| Individual 5 | -0.6708204 | 1.4342743 | 1.5652476 |
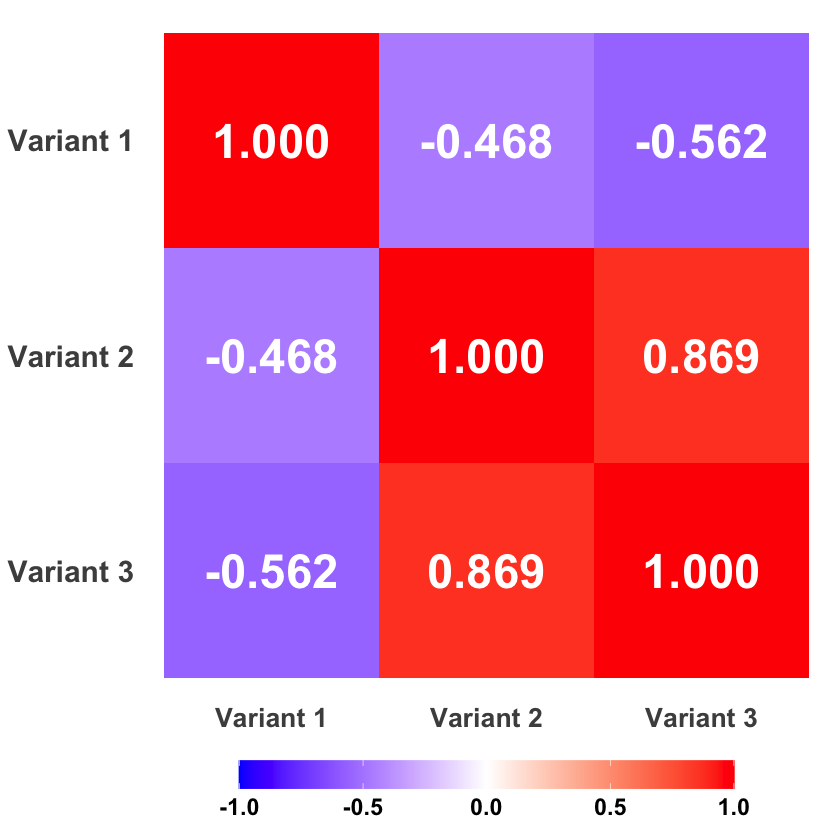
LD Matrix#
We use the cor function in R to calculate the correlation:
R = cor(X)
R
| Variant 1 | Variant 2 | Variant 3 | |
|---|---|---|---|
| Variant 1 | 1.0000000 | -0.4677072 | -0.562500 |
| Variant 2 | -0.4677072 | 1.0000000 | 0.868599 |
| Variant 3 | -0.5625000 | 0.8685990 | 1.000000 |
We also verify that the correlation matrix is identical to the covariance matrix:
cov(X)
| Variant 1 | Variant 2 | Variant 3 | |
|---|---|---|---|
| Variant 1 | 1.0000000 | -0.4677072 | -0.562500 |
| Variant 2 | -0.4677072 | 1.0000000 | 0.868599 |
| Variant 3 | -0.5625000 | 0.8685990 | 1.000000 |
Supplementary#
Graphical Summary#
# Load required library
library(corrplot)
png("/Users/serenadong/20240517_files_Rui/research_projects/statgen-primer/figures/LD_cor.png", width = 800, height = 800, res = 150, bg = "transparent")
# Create correlation heatmap with reversed order
corrplot(R, method = "color",
col = colorRampPalette(c("blue", "white", "red"))(200),
addCoef.col = "white", # Change coefficient color to white
number.cex = 2, # Make font bigger (default is 1)
number.digits = 3, # Keep 3 digits
tl.col = "black", # Text label color
tl.srt = 0, # No angle (horizontal text)
tl.cex = 1.5, # Make variable labels larger
tl.offset = 0.8, # Move top labels further up
is.corr = TRUE, # Set to TRUE for correlation matrix
order = "original", # Keep original order
cl.pos = "r", # Position color legend on right
cl.ratio = 0.2, # Make legend wider
cl.offset = 0.5, # Move legend further from the plot
addgrid.col = "white") # Set grid line width
dev.off()
corrplot 0.95 loaded
library(ggplot2)
library(reshape2)
R_melted <- melt(R)
colnames(R_melted) <- c("Var1", "Var2", "value")
# Create the plot
p <- ggplot(R_melted, aes(x = Var1, y = Var2, fill = value)) +
geom_tile() +
geom_text(aes(label = sprintf("%.3f", value)), color = "white", size = 10, fontface = "bold") +
scale_fill_gradient2(low = "blue", mid = "white", high = "red",
midpoint = 0, limits = c(-1, 1)) +
scale_y_discrete(limits = rev) +
theme_minimal() +
theme(
axis.title = element_blank(),
axis.text.x = element_text(size = 16, face = "bold"),
axis.text.y = element_text(size = 18, face = "bold"),
legend.title = element_blank(),
legend.text = element_text(size = 14, face = "bold"),
legend.position = "bottom",
legend.key.width = unit(2.1, "cm"),
panel.grid = element_blank(),
panel.background = element_rect(fill = "transparent", color = NA),
plot.background = element_rect(fill = "transparent", color = NA)
) +
coord_fixed() +
labs(fill = "Correlation")
print(p)
# Save with transparent background
dir.create("./figures", showWarnings = FALSE, recursive = TRUE)
ggsave("./figures/LD_cor.png", plot = p, width = 7, height = 6,
bg = "transparent", dpi = 150)