Hardy-Weinberg Equilibrium

Hardy-Weinberg Equilibrium#

The Hardy-Weinberg equilibrium (HWE) describes how allele and genotype frequencies remain constant across generations in a population under simple Mendelian inheritance without any interference.

Graphical Summary#

Fig

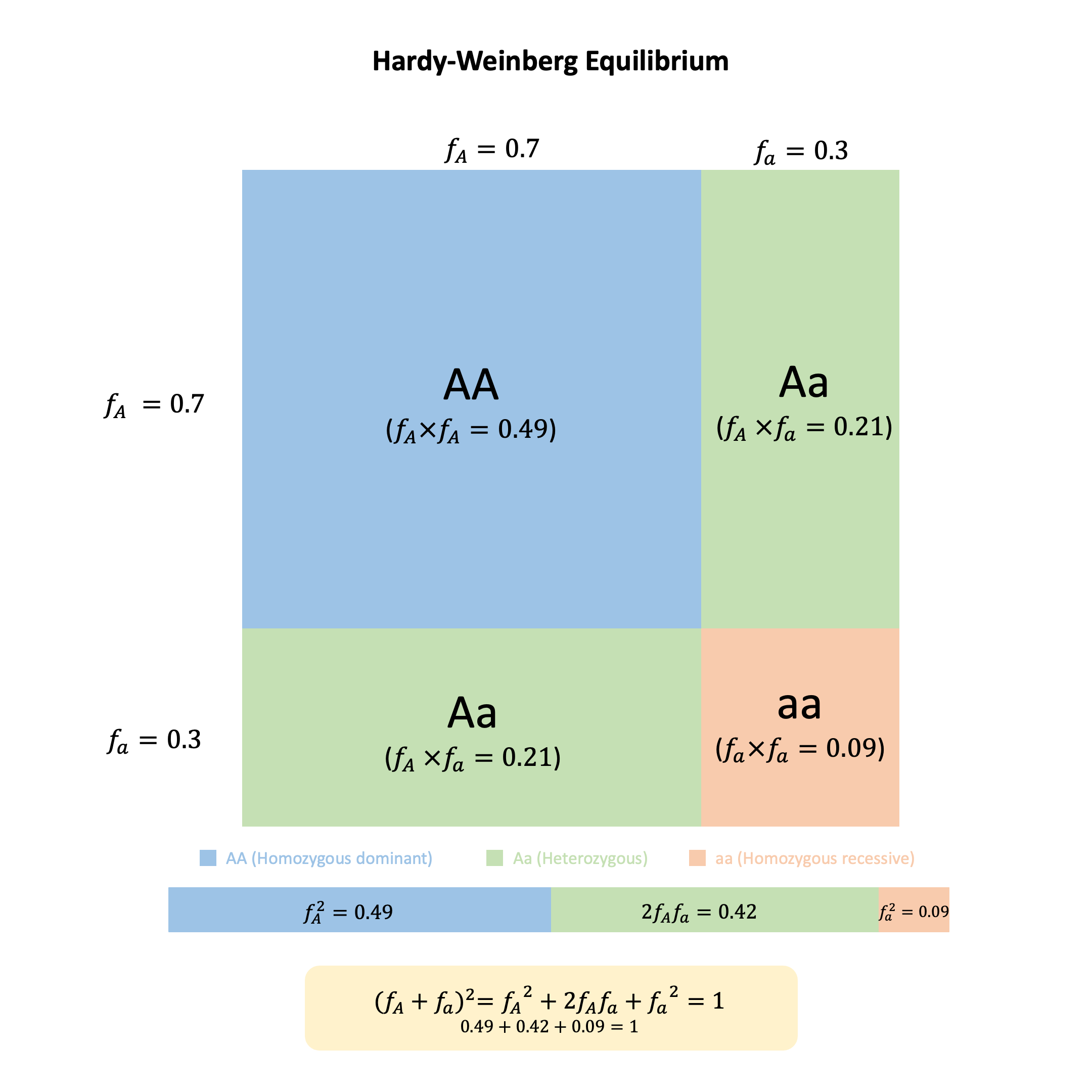
Key Formula#

For a genetic variant with two alleles (A and a) with frequencies \(f_A\) and \(f_a\) respectively (where \(f_A + f_a = 1\)):

\[ (f_A + f_a)^2 = f_A^2 + 2f_A f_a + f_a^2 = 1 \]

Where:

  • \(f_A^2\) = frequency of genotype AA

  • \(2f_A f_a\) = frequency of genotype Aa

  • \(f_a^2\) = frequency of genotype aa

HWE is fundamentally a binomial expansion with power 2. If you have two options and make the choice twice, a binomial expansion tells you the possible outcomes and their frequencies.

In HWE, we have two alleles (A and a) and choose twice (once from each parent), then the expansion \((f_A + f_a)^2\) gives:

  • The number of ways to get each genotype

  • The probability of each genotype under random mating

This structure shows HWE is about random sampling of alleles twice—exactly what happens in Mendelian inheritance.

Technical Details#

Setup a Contingency Table#

If HWE holds, it means maternal and paternal alleles are chosen independently (as in our binomial expansion). We can test this independence directly using a \(2\times 2\) contingency table.

Set up the data as:

Paternal A

Paternal a

Maternal A

AA count

Aa count

Maternal a

Aa count

aa count

Under HWE, the odds ratio should approximately equal 1.0 (which we will discuss further in Lecture: odds ratio), meaning:

  • The odds of getting allele A vs. a from the father are the same regardless of which allele came from the mother

  • Maternal and paternal allele choices are independent (exactly what our binomial expansion assumes)

When HWE Doesn’t Hold#

Common reasons why we might see deviations from HWE:

  • Non-random mating: People don’t choose partners randomly - they might prefer similar traits, leading to more homozygotes than expected

  • Population mixing: When people from different populations have children together, it can create patterns that don’t match HWE

  • Technical issues: Genotyping errors or poor DNA quality can make it look like HWE is violated

Why HWE Matters in Practice#

  • Quality control: If many genetic variants violate HWE in your dataset, it often means there are technical problems with the genotyping

  • Baseline expectation: HWE tells us what “normal” looks like, so we can spot when something interesting (or problematic) is happening

Example#

We demonstrate how to test for Hardy-Weinberg equilibrium using the classic scarlet tiger moth data in Example 1 in Lecture: odds ratio. This example shows how to set up a \(2 \times 2\) contingency table to test independence of maternal and paternal alleles, calculate odds ratios, and perform chi-square tests to determine if HWE holds in real data. Now you can skip this section.

Extended Reading#

The HWE principle is named after G. H. Hardy and Wilhelm Weinberg, who first demonstrated it mathematically.

Contents